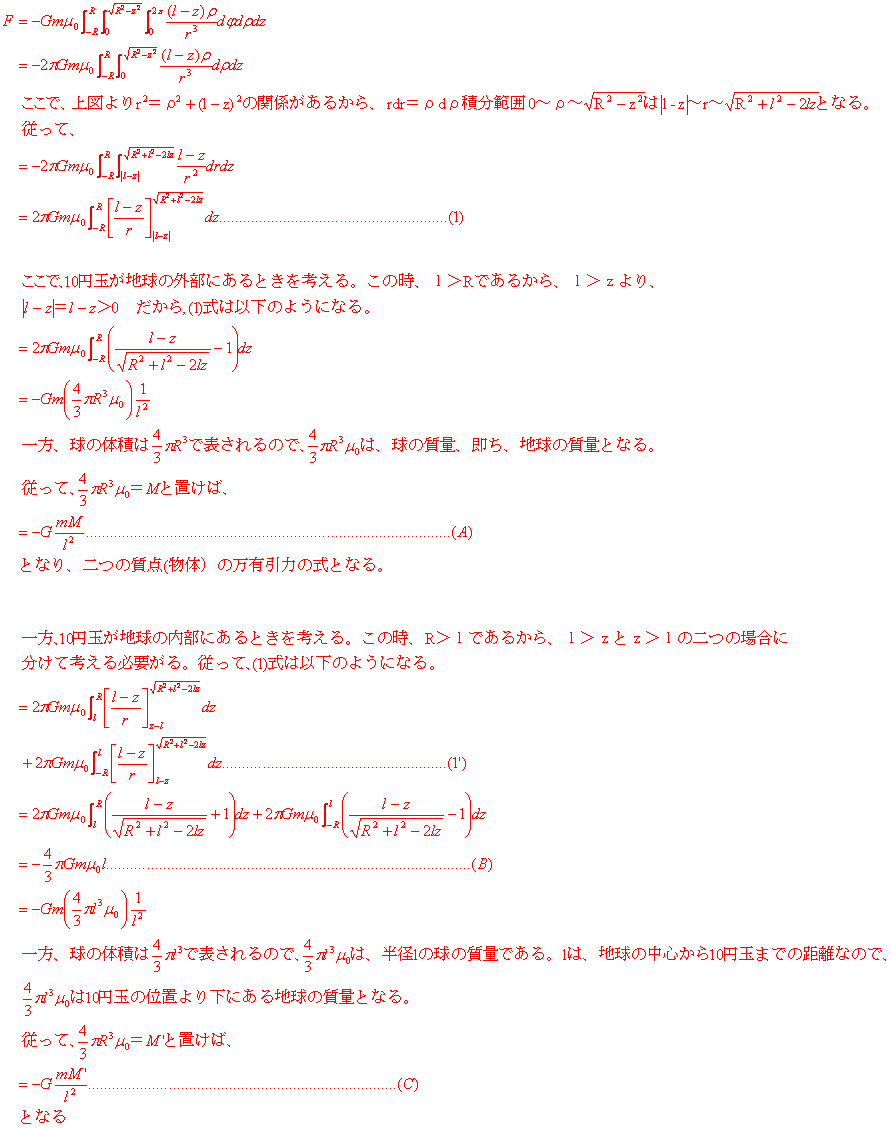地球を貫く穴に十円玉を落としたらどうなるの？
2000年5月03日に男性の方からご質問を頂きました.。
こんにちは、つまらない質問で恐縮なのですが、よろしくお願いします。実際は不可能なのでしょうが、北極から南極まで、地球を貫く穴を掘り、トンネルでも通したとします。そのトンネルに、何でもよいのですが、 例えば、１０円玉を放り込んだら、その１０円玉はどうなるのでしょう？北極から、南極まで落ちて行くのでしょうか？（それは無い？）それとも、地球の中心で浮いたまま止まるの？？？想像がつきません。教えてください。
このページに対して、8月2日と8月5日にメールを頂きました。文末に紹介の上、本ホームページを更新いたしました。
まず、「科学のつまみ食い」のホームページの中でも触れているように引力は距離の２乗に反比例して強くなることはご存知ですよね.
月の裏に月はある？
重力はどうしておきるの？
等も参考にしてください.
さて、引力で引っ張られることを考えましょう。ここでは、地球の自転に起因する遠心力を無視して考えます。
地球を細かく分割して、それぞれから受ける引力を考えます.
地球の外側にあり、地球から遠く離れたものは「細かく分割した地球」から大体同じ方向に引力を感じます。この分割された「地球の引力」を全部加え合わせると、全体として地球の方向に引っ張る力となります。この力は、地球に近づけば近づくほど距離の2乗に反比例して、強くなります。
ところで、地球の内部ではどうでしょうか?地球の中心を通り反対側へ抜けるトンネルを掘ります｡半径が約6400kmなので、トンネルの長さとしては12800kmにもなります。
さて地球表面,いわゆる地上ではどのような引力が働くでしょう｡これは先に述べた地球の外側にあるものに及ぼす引力として考えられます｡従って、分割された地球からはほぼ同じ方向である地球中心部へ向かって引っ張られる力が働きます｡
では、地球の表面から地下（下)へ400kmくらい内部に入ったところではどうでしょう?そうすると、400kmより下の部分の分割された地球は、下方向（地球の中心方向）へ引っ張ろうとしますが、400kmより上の部分は逆に上（地球の内部から表面の方向）へ持ち上げようとする力が働きます｡この内側へ引っ張る力と、外側へ引っ張る力を合わせると、まだ、内側へ引っ張る力のほうが強いです｡
次に、地球の中心ではどうでしょう｡周りには右を向いても左を見ても、上でも下でも周り全部に分割された地球があって、それぞれが外側へ引っ張ろうとします｡これら外側へ引っ張る力を合わせると、なんと引力は0になってしまいます｡従って、地球中心部で引力は働きません｡
中心を越えて更に進めば、先の400kmの時の話と同じようにまた中心へ向かって引っ張る力が働き始めます｡
これらをまとめると次のようになります｡
地球の内部にトンネルを掘った場合には、そこに働く引力は、地球の中心部では０で引力が働かないが、それ以外の場所では地球の中心へ向かって引っ張る力が働きます｡この力は、地球の表面で最も強く,内部に入るほど弱くなっていき,中心部では０になります。
このトンネルに10円玉を落とすと、10円玉は中心に向かってどんどん加速していき、地球の中心で10円玉の速度は最大になります｡中心を抜けて外へ向かうに従って、今度は逆に減速され、地球の表面では速度は０になります。するとまた、10円玉は地球の内部へどんどん落ちていきます｡
このように、地球の内部にトンネルを掘って10円玉を落とすと、10円玉は地球の中心部を中心として上下に振動する運動を永久に続けることになります｡
実はこの計算を高校生の頃にやった記憶があります。そこで、記憶を呼び戻してここで再計算してみます。
まず、条件として以下のように考えます。
地球の密度は場所によらず均一で μ0＝ 5.52g/cm3＝5.520×103kg/m3
地球の平均半径は地球を
完全な球と仮定し、赤道半径で代用すると R ＝ 6378km ＝6.378×106m
地球の北極から南極に向けて直線状に
トンネルを掘るため、遠心力の影響はない。
10円玉の質量は m ＝ 4.5g ＝4.5×10-3kg
10円玉は地球に比べ十分小さいので体積を考慮しない
地球の中心と十円玉の中心の距離を ｌ
万有引力定数を G＝6.673×10-11N m2kg-2
大気の影響を取り入れると、複雑であるため、大気の空気抵抗等を無視する。
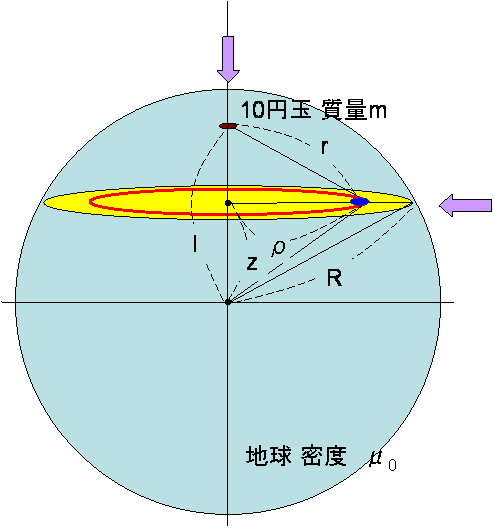
と仮定します。さて、地球、10円玉などの位置関係を下図のように考えましょう。
まず、地球の内部の点から10円玉に与える引力を考えます。
図の青色で示してある微小体積から質量mの10円玉が受ける引力 を計算します。
その微小体積はρ方向の微小変化dρとｚ方向の微小変化dzと円周方向の微小変化ｄφを用いて、
ρ dφ dρ dz
と表されます。従って、この微小体積の質量は
μ0ρ dφ dρ dz
と表されるので、10円玉（質量m）の受ける引力は万有引力定数Gを用いて 以下のように表される。（中心部へ向かう力なので、マイナスをつけてあります。)
－Gmμ0/r2 ρ dφ dρ dz
ところで、上に示した引力は縦方向の引力と横方向の引力が合成されたものです。それぞれ、全体の大きさｒに対して（ｌ－ｚ）、ρの大きさを持つので、
縦方向の引力の大きさは
－Gmμ0（ｌ－ｚ）/r3 ρ dφ dρ dz
横方向の引力の大きさは
－Gmμ0ρ/r3 ρ dφ dρ dz
となります。ところで、地球は10円玉の落ちる縦軸に対して回転対象ですから、横の軸に対する引力は左右で相殺されます。従って、縦方向のみの引力を考えれば良いことが判ります。 従って、これ以降は、縦方向のみの引力
－Gmμ0（ｌ－ｚ）/r3 ρ dφ dρ dz
を考えます。
次に、上図の赤い円から与えられる引力を考えましょう。この赤い円の円周の体積は青い微小体積をφ方向の微小変化dφについて０から２πまで一週分積分すると得られます。
更に、黄色い円盤から与えられる引力を考えます。この黄色い円盤の体積は赤い円の円周 の体積をρ方向の微小変化dρについて０から（R2-z2)1/2まで積分すると得られます。
最後に、この円盤をとｚ方向の微小変化dzを用いて ‐RからRまで積分することにより、地球全体から受ける引力が計算できます。
さて、では、その計算をしてみましょう。
さて、これらの計算結果から何がわかるでしょう？
まず、地球外部にある十円玉に働く引力は式（A)で表されるとおり
＝
となります。これは、地球の大きさを考えたにもかかわらず、その大きさによらないで、万有引力の法則が成り立つyということです。
次に、地球内部では十円玉はどのように振舞うでしょう？答えはしき（B) で表されるとおり、
となります。これは、地球の中心からの距離 ｌ が大きいほど、中心へ向かう力が強く、中心に近づくに従って、弱くなり、中心部ではその力が0になることを表しています。そして、この力は、地球の質量にはよらないで、密度だけで決まってしまいます。この式はちょうど、振り子の振動や、ばねの振動の式と同じ形をしています。ちょうどばね定数が、
の時に相当します。地球の引力によるばねの振動の振動数はいくらになるでしょう？F=－ｋｘの角振動数は√ｋ/ｍになるので、２√πGμ/3＝0.00124rad/secとなります。従って、北極から南極に貫通する穴を掘って北極の地面すれすれから十円玉を放り込むと、約2533秒（＝約42分)で、南極に達し、約5067秒（＝1時間24分)で、また北極に戻ってくることになります。そして、地球中心部では最高速度は２ｌ√πGμ/3＝7906m/secにも達します。音速が約330m/secですから20倍以上の速度、マッハ20になります。 しかし、計算上、空気抵抗を無視していますので、空気抵抗を考慮すると、かなり遅くなるはずです。空気抵抗を考慮すると、複雑になるので、今回は考慮していませんが、いずれ、時間があるときに考察してみましょう。
最後に、式(C)を考えて見ましょう。
＝
の意味するところは、計算のところでも述べたように、地球内部においては、十円玉に働く万有引力は、十円玉の位置より、内側（中心より）にある質量の影響を受け、十円玉より外側にある質量の影響を受けないことを意味しています。これは、どういうことでしょうかというと、中が空洞の球があったとします。そうすると、その球の内側では、万有引力を受けないことを意味しています。もちろん、球の外側では受けるのです。面白いですね。中が空洞の星があれば、その内部に無重力となるということですね。
さて、まとめますと、地球を貫通する穴に十円玉を落としたら、その十円玉は単振動を永遠に繰り返すということですね
地球を貫く穴に十円玉を落としたらどうなる？に2002年8月2日に以下のようなメールを頂きました。
地球を貫く穴に十円玉を落としたらどうなるの？を読ませていただきました。 空気抵抗についての仮定を記入していないように思います。 もっとも、空気がトンネル内にあれば、まっすぐ落ちない・まっすぐ落ちても音速を越えない・中心部は引力が０でも大気圧は高い 等、あまりにも大前提で記入されなかったのかもしれませんが。
メールありがとうございます。
そうですね。空気抵抗についての過程が入ってないですね。計算上空気抵抗は無視
していますが、時間があれば空気抵抗を考慮して考察してみます。
ご意見ありがとうございました。
地球を貫く穴に十円玉を落としたらどうなる？に2002年8月５日に更に以下のようなメールを頂きました。
８／１の１０円玉の件ですが
初速 ８ｋｍ／ｓｅｃ（中心部での最高速度）の等速運動としても ６４００ｋ
ｍ移動するには ８００ｓｅｃかかる
と思うのですか・・・．
６４ｓｅｃと８ｋｍのどちらかが 間違っているのでは？
と思いました．
では また・・・．
メールありがとうございます。御指摘の通り、時間の計算ミスです。時間を出すのに0.00124rad/secの逆数に２πをかけなければならないところを２πで割ってしまってました。64秒、128秒ではなく、 その４π2倍の2533秒、5067秒です。御指摘ありがとうございました。
今後ともよろしくお願いいたします。