|
by I-satto@03/11/02
2002年12月3日 と2003年2月4日にバルブ会社の 技術の方からご質問を頂きました.。
いつもお世話になっています。
弊社はバルブ会社ですが、この度高温用のバルブの製作検討中です。
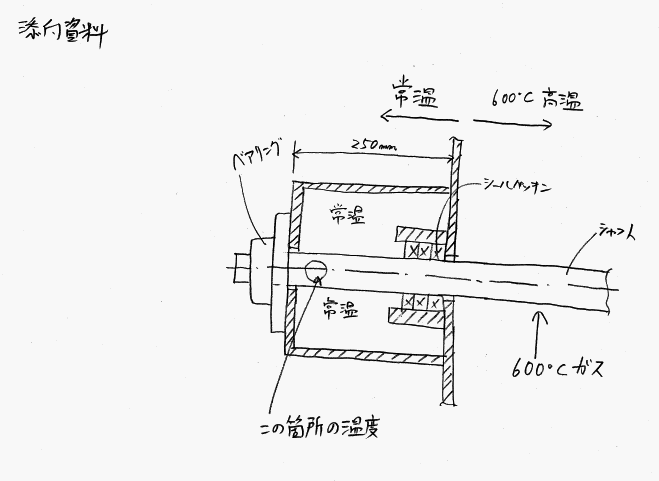
その中でシャフトの材質をSUS304かSS400で検討中ですが添付資料の軸受下の箇所の伝わる温度は最終的にはどちらの方が低くなるのでしょうか?熱伝導率の小さいSUS304の方が低くなるのですか?
お手数ですが御教え下さい。

いつもお世話になっています。
先回の熱伝達についてのご教示ありがとうございました。
誠に申し訳ありませんが、熱伝達についてもう少し教えてください。
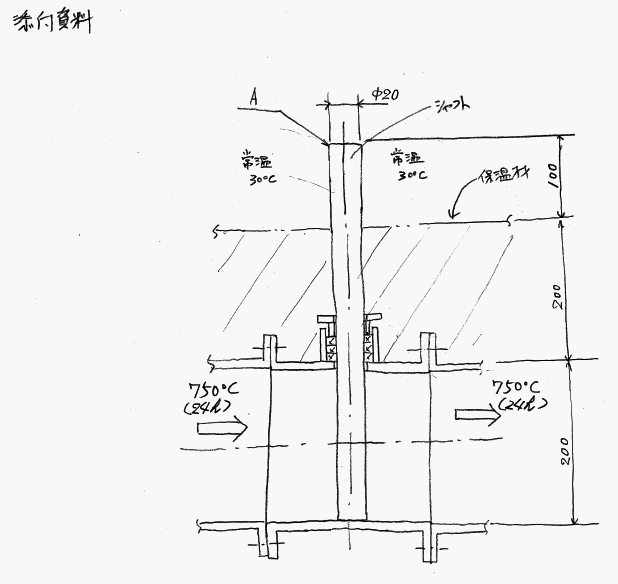
添付資料よりダクト管内に750℃の熱風が常時24h流れている時、SUS316Φ20のシャフトのA部の温度は約何度になりますか?ダクト表面から200mmの厚さで保温材が巻いてあり、100mm常温で外部にさらされます。基本的に保温材部は放熱されません。
お手数ですが宜しくお願いします。もしよろしければ計算式がありましたら教えてください。
1.シャフトが流体内に突き出ていないモデル
(1)1次元化
(2)定常状態
(3)熱伝達率
(4)仮定は正しいか?
2.シャフトが流体内に突き出ているモデル
(1)1次元化と定常状態
(2)熱伝達率
(3)熱伝導率の違い
3.シャフトが流体内に突き出ていないモデルと突き出たモデルの比較
4.解の整理
(1)シャフトの熱伝導の1次元定常解
(2)シャフト底面の熱伝達率
(3)シャフト側面の熱伝達率
(4)使用した定数
1.シャフトが流体内に突き出ていないモデル
(1)1次元化
まず、モデルの簡略化をします。この問題の場合、シャフトの断面の温度を求めることです。また、断熱材でシャフト部が覆われているので、断熱材方向へは熱は逃げないと仮定できます。従って、この問題を1次元問題としてときます。最初は、簡単のためにシャフトが流体内に突き出ていないと仮定します。
即ち次の図のようなモデルを考えます。
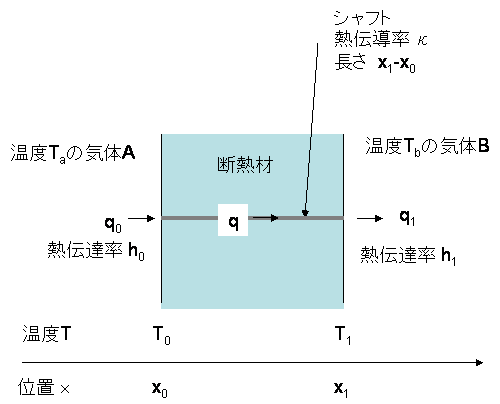
このとき、x軸方向しか考えないので、解くべき式は
![]()
と、1次元化されます。
境界条件は、両側T0及びT1の温度の気体による熱流量q0、q1で与えられます。
(2)定常状態
ところで、この問題では、目的場所の温度を求めることが最終目標です。目的場所は熱源から離れているので、徐々に温度が上がって、一定温度になると考えられます。そこで、定常状態になったときの温度を計算します。この場合は、上の式において、時間変化が0ということになります。
即ち
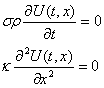
です。
これで式は、かなり簡単になりました。ここで、時間変化は考えないので、解くべき方程式は位置による分布のみですから

にだけ着目すれば良いことがわかります。
さて、この式を1回だけ積分すると
![]()
となります。これは、「科学のつまみ食い」の「熱伝導率が金属によって異なるのはなぜ? 」で、示した熱伝導の式に帰着します。これは、フーリエの式とも呼ばれます。ここで、定数は熱の移動になるはずですから、qと置きます。
![]()
これを解けば、
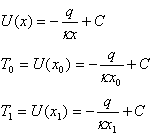
となります。但し、
Cは積分定数です。
ところで、この場合、温度Taの気体からシャフトに熱が移動し、シャフトからは温度Tbの気体に熱が移動します。これを熱伝達といいますが、伝わる熱量は伝える物質と伝えられる物質(この場合、空気とシャフト、シャフトと空気)の温度差に比例します。単位面積当たり単位時間に単位温度差当たりに伝達させる熱量を熱伝達率と
言います。この熱伝達率を、それぞれh0、h1としますと、それに比例した熱量がシャフトを伝わって流れます。
今、定常状態を仮定していますので、温度Taの気体からシャフトに入ってくる熱量q0とシャフトから温度Tbの気体へ出て行く熱量q1は等しくなります。また、先の熱伝導の式でわかるとおり、シャフト内はどこでも同じ熱量qが伝わります。そこで、

ここから、T0,T1を消去すれば
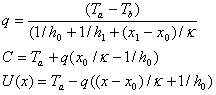
となります。
これが求める定常状態における式です。
整理すると

あとは、それぞれの定数を調べればよいです。
SUS316F20の熱伝導率
κ:16.4W/mK
気体Aの温度
Ta:750℃
気体Bの温度
Tb:30℃
シャフトの端の位置
x0:0:0cm
気体Aとシャフトが接するところの熱伝達率
h0:
気体Bとシャフトが接するところの熱伝達率
h1:
さて、上では、熱伝達率がわかりませんので、これは、次のようにして求めます。
(3)熱伝達率
ところが、ここで問題になるのは、熱伝達率です。今回の問題の場合は、気体から固体へ、固体から気体へ流れる熱伝達率を求める必要があります。これは、気体の流れる速度などに依存します。今回いただいたデータでは、それらの情報が不足していますので、ここでは、それらを仮定して進めます。
また、気体の流れが自然対流(空気が自然に流れる)の場合は熱伝達率が固体の温度に依存しますので、今回のように、熱伝達率が固体の温度に依存しないという仮定の下でといた場合と解が異なります。従って、ここでは強制対流(空気を強制的に流す)の場合のみを考えます。
強制対流の場合、その流れは規則正しく流れる層流と流れが不規則な乱流に区別されます。これはレイノルズ数に依存します。平板表面を流れる流体のレイノルズ数は限界レイノルズ数というのがあり、それ以上になると層流を保てなく
なり、乱流になるといわれています。通常、限界レイノズル数は1x105〜5x105程度といわれています。
レイノルズ数Reは以下のように表されます。

さて、今考えている2番目の問題では、シャフト(但し、この場合はシャフトは突き出ていないと仮定されています)の両端に750℃の空気と30℃の空気が流れていますから、次のようにレイノルズ数を計算します。温度800℃(750℃のデータが見つからなかったので800℃で仮定しました)、空気の流れの速度1m/s、代表長さ15.7mm(直径φ20mmより平均長さ πr/2 を求める)とすると、動粘性係数は1.37x10-4m2/sとなるので、レイノルズ数は114.7となり、層流となります。また、温度20℃(30℃のデータがっ見つからなかったので20℃で仮定しました。)の場合は、動粘性係数は0.156x10-4m2/sとなるから、レイノルズ数は1007となり、こちらも層流となります。従いまして、ここでは空気の流れは層流として扱います。ちなみに、このサイズですと流速が100mを超えなければ乱流にはなりません。
層流の場合、熱伝達率はレイノズル数とプラントル数を使用して以下の式で表されます。

ここで、レイノルズ数とプラントル数について簡単に説明しておきます。
この問題では空気とシャフトの間の熱伝達を考えていますが、この熱伝達で、今まで、熱伝達率としてhを使用してきました。今、流れを代表する寸法を L(代表長さ)、流体の熱伝導率を λ としたときにNu=hL/λ で定義される無次元数をヌッセルト数 Nusselt number と呼びます。このヌッセルト数を次元解析すると、強制対流の場合には、同じく無次元数であるプラントル数 Prandtl number(流体の粘性率を μ,定圧比熱を cp, 重力加速度を gとして,cpμg/λ で定義される)とレイノルズ数の関数に,また自然対流の場合にはプラントル数とグラスホフ数 Grashofnumber(重力加速度を g,流体の動粘性率を ν,熱膨張率を β として L3βgΔT/ν2で定義される)の関数になることが判っています。ここでは、強制対流の層流を扱っていますので、そこから、熱伝達率はレイノルズ数とプラントル数の関数で表されます。詳しくは熱伝導等の解説書などに記載されていますので、それを参考にしてください。
さて、 温度800℃のレイノルズ数は先の計算より114.7と計算されましたが、プラントル数をを計算しなければなりません。

このように、プラントル数Prは0.715となります。代表長さ15.7mm、空気の熱伝導率7.07x10-2W/mKとなるので、
h0=2.86x10-3W/cm2K
となります。一方、温度20℃のレイノルズ数は先の計算より1007、プラントル数は

より0.711で代表長さ15.7mm、空気の熱伝導率2.57x10^-2W/mKとして
h1=3.08x10-3W/cm2K
となります。
ちなみに、乱流の場合の熱伝達率は
h=0.0365 Re0.8 Pr λ/L
であらわされ、垂直平板の自然対流(層流)の場合の熱伝達率は
h=0.479 g L3(T1-Tb)/ν2 λ/L
であらわされます。
ここで、
g :重力加速度
T1:固体の温度
Tb:流体の温度
さて、 ここで、問題に戻ります。

SUS316F20の熱伝導率
κ:16.4x10-2W/cmK
気体Aの温度
Ta:750℃
気体Bの温度
Tb:30℃
シャフトの端の位置
x0:0cm
x1:20cm
気体Aとシャフトが接するところの熱伝達率
h0:2.86x10-3W/cm2K
気体Bとシャフトが接するところの熱伝達率
h1:3.08x10-3W/cm2K
とすれば、
U(x)=434-5.51x
となります。30℃の空気と接しているx1=20cmの位置のシャフトの温度は322℃になります。
(4)仮定は正しいか?
さて、ここで注意しなければならないのが、熱伝達率です。ここでは、熱伝達率を求めるのに多くの仮定を導入しました。従って、この解が熱伝達率に大きく依存する場合には求めた値を使用するのには注意する必要があります。

ですから、1/h1が小さいほど、即ちh1が大きいほど、x1における温度Vが下がることを示しています。
例えば、30℃の空気の流速を10m/s(10倍)にすると、レイノルズ数は10070となり、熱伝導率はh1=9.74x10-3W/cm2Kとなります。従って、端面での温度はU(x)=311−7.64x、x=x1=20cmから、159℃になります。
逆に、30℃の空気の流速を0.1m/s(10分の1)にすると、レイノルズ数は100.7となり、熱伝導率はh1=9.74x10-4W/cm2Kとなり
ます。従って、端面での温度はU(x)=582−2.93x、x=x1=20cmから、523℃になります。
このように流体で冷却する場合の問題は熱伝導率とともに熱伝達率に大きく依存することがわかりました。従って、上のモデルでは、空気とシャフトの接する面積に関してシャフトの端面しか考慮せず、シャフトの側面について取り入れていないので、モデルとしてはかなり無理があ
る事が判ります。