|
by I-satto@03/11/02
2002年12月3日 と2003年2月4日にバルブ会社の 技術の方からご質問を頂きました.。
いつもお世話になっています。
弊社はバルブ会社ですが、この度高温用のバルブの製作検討中です。
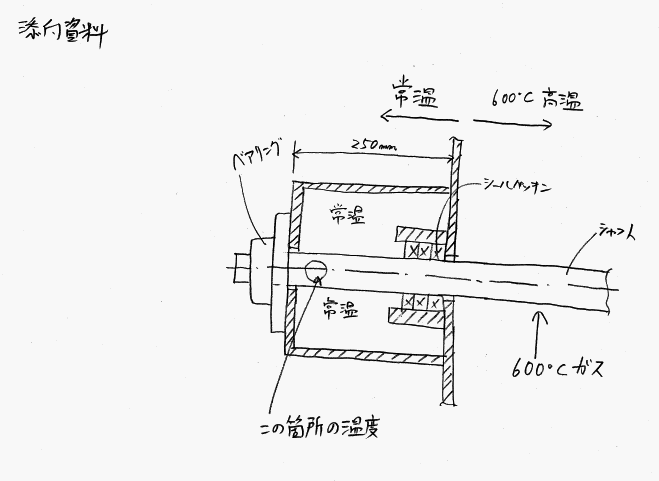
その中でシャフトの材質をSUS304かSS400で検討中ですが添付資料の軸受下の箇所の伝わる温度は最終的にはどちらの方が低くなるのでしょうか?熱伝導率の小さいSUS304の方が低くなるのですか?
お手数ですが御教え下さい。

いつもお世話になっています。
先回の熱伝達についてのご教示ありがとうございました。
誠に申し訳ありませんが、熱伝達についてもう少し教えてください。
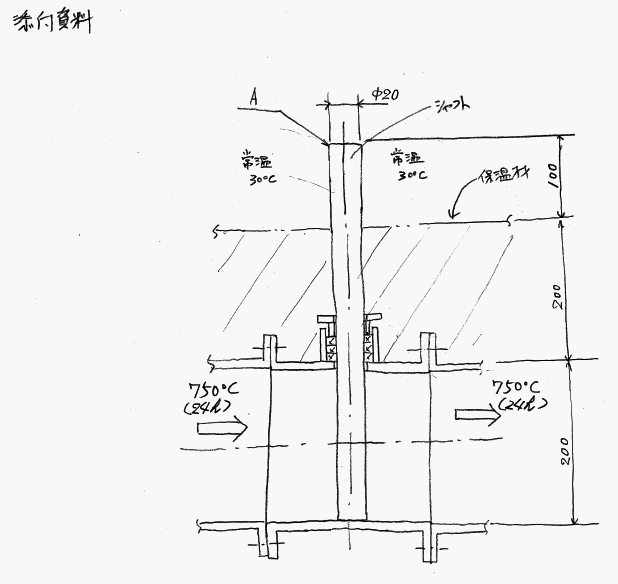
添付資料よりダクト管内に750℃の熱風が常時24h流れている時、SUS316Φ20のシャフトのA部の温度は約何度になりますか?ダクト表面から200mmの厚さで保温材が巻いてあり、100mm常温で外部にさらされます。基本的に保温材部は放熱されません。
お手数ですが宜しくお願いします。もしよろしければ計算式がありましたら教えてください。
1.シャフトが流体内に突き出ていないモデル
(1)1次元化
(2)定常状態
(3)熱伝達率
(4)仮定は正しいか?
2.シャフトが流体内に突き出ているモデル
(1)1次元化と定常状態
(2)熱伝達率
(3)熱伝導率の違い
3.シャフトが流体内に突き出ていないモデルと突き出たモデルの比較
4.解の整理
(1)シャフトの熱伝導の1次元定常解
(2)シャフト底面の熱伝達率
(3)シャフト側面の熱伝達率
(4)使用した定数
2.シャフトが流体内に突き出ているモデル
(1)1次元化と定常状態
さて、先のモデルでは無理があり、不十分なので、最初のモデルをもう少し現実に近づけてみます。
最初のモデルは流体(空気)中にシャフトが飛び出ていないと仮定しました。
今回はシャフトが飛び出ているモデルにします。
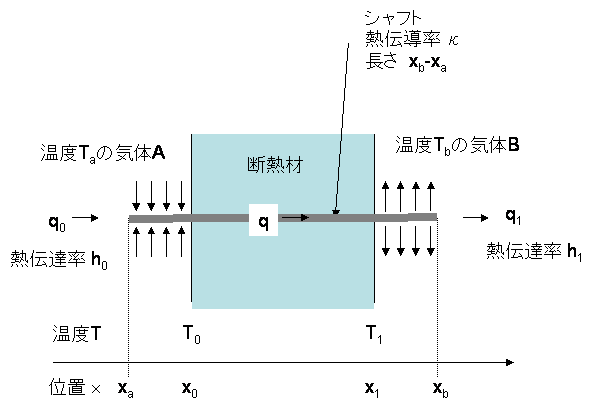
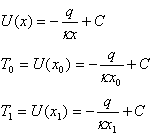
ここまでは、シャフトが突き出ていないモデルと同じです。
(2)熱伝達率
さて、このモデルでも温度Taの気体からシャフトに熱が移動しますが、このとき、流体が接する円柱の底面部と円柱の側面部から熱が伝達します。熱伝達率は流速やその形状によって大きく変化
するのは、上に述べたとおりですので、ここでは、円柱の底面部と円柱の側面部二つの部位に分けて考えます。シャフトから温度Tbの気体に熱が移動する場合も同様です。これらの熱伝達率を、それぞれh0a、h0b、h1a、h1bとしますと、それに面積をかけた分だけの熱量がシャフトを伝わって流れます。先のシャフトが突き出ていない場合は断面が同じなので、単位面積あたりの熱の移動を考えました
が、今回は伝わる面積が異なります。
Taの流体に接しているところの面積は
円柱底面部:πr2
円柱側面部:2πr(x0-xa)
断熱材で巻かれたところの断面積:πr2
Tbの流体に接しているところの面積は
円柱底面部:πr2
円柱側面部:2πr(xb-x1)
今、定常状態を仮定していますので、温度Taの気体からシャフトに入ってくる熱量q0とシャフトから温度Tbの気体へ出て行く熱量q1は等しくなります。また、先の熱伝導の式でわかるとおり、シャフト内はどこでも同じ熱量qが伝わります。そこで、

さて、この式を次のように書き換えます。
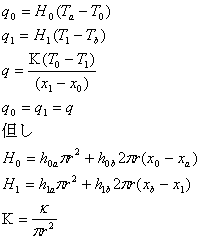
これらより、最初のシャフトが突き出ていない場合の熱伝達率hをHに、熱伝導率κをΚに書き換えたものであることが判ります。
従って、その解は以下のようになります。

さて、シャフトの底面部の熱伝達率はは円柱底面として平板の熱伝達率を用います。これは、最初に計算したものと同じものを使用しますが、ここに再掲しておきます。
先の計算と同様ですので、空気の流れは層流として扱うことができます.
温度800℃(750℃のデータが見つからなかったので800℃で仮定しました)、空気の流れの速度1m/s、代表長さ15.7mm(直径φ20mmより平均長さ
πr/2
を求める)とすると、動粘性係数は1.37x10-4m2/sとなるので、レイノルズ数は114.7となり、プラントル数は0.716で
となるので、空気の熱伝導率7.07x10-2W/mKとすると、h0a=2.86x10-3W/cm2Kとなります。
一方、温度20℃(30℃のデータがっ見つからなかったので20℃で仮定しました。)の場合は、動粘性係数は0.156x10-4m2/sとなるから、レイノルズ数は1007となり、プラントル数は0.711で、空気の熱伝導率2.57x10-2W/mKと
すると、h1a=3.08x10-3W/cm2Kとなります。
一方、シャフトの側面は、円柱側面の熱伝達率を用います。これは実験式として以下のように与えられます。
層流の場合(0.1<レイノルズ数<1000)
h=(0.35+0.47Red0.52)Pr0.3 λ/2r
乱流の場合(1000<レイノルズ数<50000)
h=0.26Red0.6 Pr0.3 λ/2r
円柱側面のレイノルズ数Reは

であらわされますから、
温度800℃(750℃のデータが見つからなかったので800℃で仮定しました)、空気の流れの速度1m/s、半径10mmとすると、動粘性係数は1.37x10-4m2/sとなる
ので、レイノルズ数は146となり、層流となります。
このとき、プラントル数は0.715で半径10mm、空気の熱伝導率7.07x10-2W/mKと
すると、h0b=2.12x10-3W/cm2Kとなります。
一方、20℃(30℃のデータがっ見つからなかったので20℃で仮定しました。)、空気の流れの速度1m/s、半径10mmとすると、動粘性係数は0.156x10-4m2/sであるから、レイノルズ数は1282となり、こちらは乱流となります。
このとき、プラントル数は0.711で半径10mm、空気の熱伝導率2.57x10-2W/mKと
すると、h1b=2.21x10-3W/cm2Kとなります。
従って、整理すると、それぞれの熱伝達率は以下のようになります。
h0a=2.86x10-3W/cm2K
h0b=2.12x10-3W/cm2K
h1a=3.08x10-3W/cm2K
h1b=2.21x10-3W/cm2K
このとき、
πr2=3.14 cm2
2πr(x0-xa)=125.7 cm2
2πr(xb-x1)=62.8 cm2
ですから、
H0=0.275 (H0/πr2 =8.77x10-2W/cm2K)
H1=0.149 (H1/πr2 =4.75x10-2W/cm2K)
Κ=0.515 (Κ/πr2 =16.4x10-2W/cm2K)
となるので、
U(x)=697-28.4x
となり、x=x1=20cmの部分の温度は、129℃となります。最初に求めたシャフトが流体内に突き出ないモデルの温度322℃よりはかなり温度が下がります。
ちなみに、30℃側の空気の流速が10m/sと0.1m/sの場合について計算してみますと、
例えば、30℃の空気の流速を10m/sにすると
H1=0.5833
となり、
U(x)=691−31.6x
x=x1=20cm
のときは、58℃になります。
逆に、30℃の空気の流速を0.1m/sにすると
H1=0.0379
となり、
U(x)=712−20.3x
x=x1=20cm
のときは、306℃になります。
(3)熱伝導率の違い
今まで、SUS304Fを考えていましたが、
ここで、熱伝導率の違いによってどのような違いが出るか計算してみましょう. ここではSS400を対象として考えて見ます。
SS400の熱伝導率は
κ=60.6x10-2W/cmK
ですから、上の
U(x)=697-28.4(x-x0)
に対応する答えは、
U(x)=624-18.1(x-x0)
となり、x=x1=20cmの部分の温度は、262℃となります。従って、熱伝導率が高いと温度が高くなってしまいます。(最初の質問の答え)。
これは、元の発生する熱量が同じで、除熱する熱量が同じならば、熱は、その伝導する物質、ここではシャフトですが、にたまることになります。熱伝導率が小さければ、熱の発生元と発散先の温度差が大きくなり、逆に熱伝導率が大きければ、熱の発生元と発散先の温度差が小さくなるということです。