基礎編
by I-satto@27 May, 1999
どこの家庭にでもあるビデオカメラは1秒間に30コマの撮影ができますから、1/30秒間隔で運動を撮影、計測することが可能です。今回は1999年5月9日に当時小学2年生の長男に手伝わせて、DV(デジタルビデオカメラ)でボールの落下運動を撮影し、重力加速度を測定しました。昔は家庭では1/30秒を測定することなんてできなかったんですけどねぇ
【重力って?】
地球の上の物が地球から受ける力で、万有引力と地球の自転による遠心力とを合わせた力です。地球上の場所によって多少違う値を取ります。赤道の近くが最も小さくなります。ところで、万有引力というのはすべての物体の間で引き合う力です。その大きさは質量の積に比例して距離の二乗に反比例します。ニュートンにより発見されました。りんごが落ちる話は有名ですね。そこで、ここでは、重力加速度を測定します。では、重力加速度って何でしょう? 物に働く重力をその物の質量で割ったものです。その値は地球上の位置・高さによって異なります(万有引力が距離の2乗に比例することから判ると思います。概略の値は約9.81m/s2です。
【重力加速度を測定しよう】
では、重力加速度測定してみましょう。
【準備するもの】
(画像をクリックすると大きくなります。
| ビデオカメラ |
 |
ここでは、PanasonicのDV-NS7を使用しました。DV(デジタルビデオ)カメラを使用することにより、画像をパソコンに取り込んでデータを処理できる利点があります。アナログビデオカメラとかDVCでパソコンを使用しなくても、撮影したビデオをテレビにコマ送りで映し出して、画面上で落下距離などを定規で測定しても重力の測定は十分可能だと思います。精度はかなり落ちるかもしれません。.ちなみに、1コマ1/30秒(0.033333sec)ですから、これはお間違えないように!!。 |
| ボール |
 |
落下させるものは、何でも良かったのですが、丸いもののほうが後々のデータ整理がやりやすいのと、大きいものの方がビデオ写りが良いために、当時小学2年生の長男のドッジボールを使用しました。ここで、唯一大事なのが、このボールの直径を測定しておくことです。落下した高さを測定するよりも楽ですし,このボールの直径を基準にして落下距離もわかりますから(^^)。ということで、このボールの直径は19cmでした。 |
| 三脚 |
 |
三脚を使用してビデオをきちんと固定しましょう。高々1秒程度の撮影ですが、これにより画面のぶれが少なくなり、重力加速度の測定が正確になります。横に写っているのはレリーズですが、ビデオ撮影にはまったく必要ありません(^^ゞ。この画像は、日食の写真を撮ろうで使った画像を使いまわしているだけだったりしますから(^^ゞ。 |
| 高いところ |
 |
さて、高いところが必要です。重力加速度が9.81m/s2ですから、1秒間に4.9mほど落下します。しかし、ビデオカメラのフレームレートが30fps(1秒間に30コマ)ですから、データとしては20個もあれば十分です。そうすると、0.7秒くらいの撮影で良いですから、2.5mくらいの高さでで十分です。今回は左の写真に見られるように、私の自宅の2階のベランダからボールを落としました。当時小学2年生の長男の顔は見えないですが、良く見るとボールを落とす手は見えています。布団が干してあったり、車が見えてたりあまり綺麗ではないですが、計測ですから十分です(^^ゞ。ところで,カメラアングルはボールを落とすところから、地上まで入るようにちょっと離れてましょう。 |
【重力を測定しよう】
| では、重力の測定です。上に述べたように、自宅の2階のベランダに当時小学2年生の長男を立たせ、ベランダの手すりにボールを置き(上の写真のように)、私は庭に降りて右の写真のように三脚に載せたデジタルビデオカメラ設置します。ビデオカメラでボールと落下地点の地面が入るように、ズームや距離をあらかじめ決めて置きます。ビデオをスタートして、その後に息子にボールを押すように指示します。ボールが落下したら、ビデオを止めるだけです。非常に簡単でしょう(^^)。あとは、撮影されたビデオからデータを整理するだけです。こちらのほうが大変かもしれません。 |
 |
【データを整理しよう】
こういう物理実験では、実験のアイデアとそのデータ整理が重要です、今回の重力測定でのアイデアは、家庭用ビデオカメラを使用して実験できるということがポイントです。データ整理は結構大変ですが、ビデオを使っていることで直感的に判るかもしれません。
【ボールが落ちるのをコマ送りで見よう】

|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| アニメーション |
0.0sec |
0.1sec |
0.2sec |
0.3sec |
0.4sec |
0.5sec |
0.6sec |
0.7sec |
0.8sec |
0.9sec |
まずは、撮影したビデオを見てみましょう。大画面のテレビがあればそれに接続してみるのが一番判りやすいです。まずは、通常再生、スロー再生、コマ送りと順番に見てみましょう。左にはビデオカメラからパソコンに取りこんだ画像を示して置きます。最も左端の画像は、落下時のアニメーションでスロー再生されています。その右には、取り込んだ画像を0.1秒ごとに分解した写真を載せました。この写真はほぼ等間隔で並んでいるので、ボールが落ちるに従って、ボールの落ちる距離が長くなっていくのが判るでしょう。このビデオや分解写真ではわからない正確なデータを得るために、ビデオをコマ送りで再生しながらデータを取っていきます。落下距離はボールの直径を基準にしてボールの直径の何倍の距離を落下したか記録していきましょう。時間は、1コマで1/30秒経過しますので、2コマ目で1/30秒経過、3コマ目で2/30秒経過します。これで、ボールが落下する場合の経過時間に対する落下距離のデータが出来上がります。ちなみに、私のようにパソコンでビデオ映像を取りこむこ
とのできる環境がある人は、実際の取り込んだデータを用いて、画像から落下距離と時刻のデータを作成するのが良いでしょう。もちろんこの時は画像のピクセルを単位にし、落下距離はボールの大きさを基準に整理するとよいです。
|
| 【落下速度と経過時間をグラフにして見ましょう.】 |
|
この右の表は2つの隣り合った画像間の落下距離と落下速度(画像間のボールの落下距離の差を画像間のの落下時間の差で割ったもの)、そして、その経過時間(画像間の平均時間)を記したものです。通常,学校の授業などで重力加速度を測定する場合に対応しますが、今回のビデオの撮影ではちょっと判りにくいかもしれません。もっと判りやすく図で説明しましょう。上の分解写真の0.5秒の時と0.6秒の時の2つの画像に注目してください。この2つの画像のボールの距離は51cmです。この51cm進むのに0.1秒かかっていますので、この時の平均速度は5.1m/sになります。この時の時刻は0.5秒と、0.6秒の間を取って0.55秒とします。このようにして、落下の平均速度とその時の経過時刻を求めて表にしたものが右の表なんです。これで判りましたか?(ちなみに、右の表は1/30間隔で表にしました。
下の図はこの表をグラフにしたもので、●が落下速度で■が測定された1/30秒の間に落下した距離です。これが最も直感的にわかりやすいグラフになります。この図から、落下速度(落下距離)は経過時間に比例することがわかります。この落下速度が単位時間(1秒間)増加する割合(グラフの傾き)が加速度と呼ばれるもので。この場合は重力加速度になります。このグラフに直線を引いて、その傾きを求めると9.78m/s2という値が得られます。これが重力加速度の測定値です。実際の値9.81m/s2と良く一致しています。こんな簡単な実験でも1%以下の精度で重力加速度が求められます(^^)
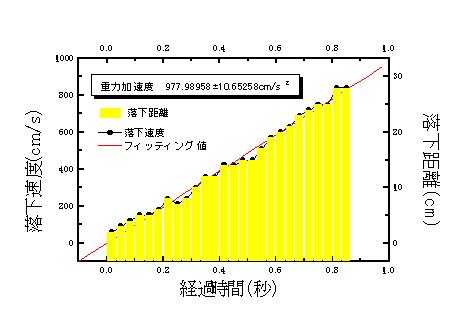
|
さて、このことから、重力(g)によって速度(v)は時間(t)に比例して増えていく(v=gt)、そして、その増える割合は一秒間に9.78m/sの速度だけ増え,それを重力加速度といい、その値は9.78m/s2であることが判りました。ところで、上のグラフの■は、もともと、1/30秒間に落下した距離ですから、この棒グラフの和(棒を全部足した値)は落下し始めた最初の時刻(0秒)からの落下距離全体になります。要するに■の部分の面積が落下距離になります。そこで、全体の落下距離は、この■で区切られた三角の領域の面積です。従って、その面積を計算すれば、底辺(t)掛ける高さ(v)割る2が三角形の面積ですから、落下距離(h)はその時の落下速度(v)と時間(t)を掛けたものを2で
割った値に等しい(h=vt/2)という法則が判りました。
| v=gt |
落下速度は重力加速度に落下時間を掛けた値に等しい |
| h=vt/2 |
落下距離はその時の落下速度に落下時間を掛けて2で割った値に等しい |
| h=gt2/2 |
落下距離は重力加速度に落下時間の2乗を掛けて2で割った値に等しい |
|
落下距離
の差(cm) |
落下速度
(cm/s) |
経過時間
(s) |
| 2 |
60 |
0.0167 |
| 3 |
90 |
0.05 |
| 4 |
120 |
0.0833 |
| 5 |
150 |
0.1167 |
| 5 |
150 |
0.15 |
| 6 |
180 |
0.1833 |
| 8 |
240 |
0.2167 |
| 7 |
210 |
0.25 |
| 8 |
240 |
0.2833 |
| 10 |
300 |
0.3167 |
| 12 |
360 |
0.35 |
| 12 |
360 |
0.3833 |
| 14 |
420 |
0.4167 |
| 14 |
420 |
0.45 |
| 15 |
450 |
0.4833 |
| 15 |
450 |
0.5167 |
| 17 |
510 |
0.55 |
| 19 |
570 |
0.5833 |
| 20 |
600 |
0.6167 |
| 21 |
630 |
0.65 |
| 23 |
690 |
0.6833 |
| 24 |
720 |
0.7167 |
| 25 |
750 |
0.75 |
| 25 |
750 |
0.7833 |
| 28 |
840 |
0.8167 |
| 28 |
840 |
0.85 |
|






