太陽の周りを回る月の軌道について？

1999年10月22日に天文ファンの男性からご質問を頂きました.。 

　はじめまして。いつも興味深くこのホームページを見させていただいています。私は、天文を趣味としている者です。仲間と同好会を作って、まあ適当に活動しています。市などから要請があれば、ボランティア活動として、観望会を開催しています。
　それは今年６月に行った観望会でのことでした。あいにく天気が良くなかったので室内で天文の講義を行いました。そこで一人の男性から質問があったのですが明解な返答をすることができませんでした。そこでお願いです。以下の質問に、私でも分かるように答えていただけると嬉しいのですが・・
　まず質問を明解に説明することができるかどうか不安ですが、できる限り詳しく述べてみます。
　その質問とはこうです。
　ご存知のように地球は太陽の周りを公転しています。そして月は地球の周りを公転しています。月は一回公転する間に、地球の軌道より内側に入り込んだり、外側に出たりしています。それで、月が地球の周りを公転する軌跡を描いて調べてみると、月が地球の軌道の内側にいる長さと、外側にいる長さが異なっているように見えます。（外側のほうが長い？）これはなぜでしょうか？
　私はその人に分かるように説明することができませんでした。
　ではよろしくお願いします。。

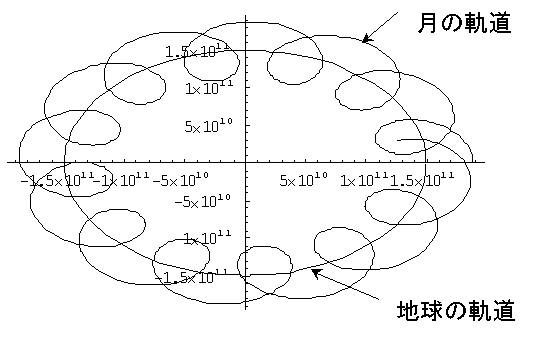
　月の軌道を太陽を中心に描いていくと、下の図の様にらせん状になり、そのとき,月の軌道の軌跡は、地球の軌道の外側のほうが長く、地球の軌道の内側のほうが短くなると言うことですね。

　月が地球の周りを回っていると考えれば、円の軌道ですが、地球は太陽の周りをも回っていますから、月も太陽の周りを回っています。従って、上の図の様に月は太陽の周りをらせん状に回る 様に思えますが、実は月はらせん状には回らず、地球の公転軌道と同じ方向に、それと垂直に太陽のほうへ寄ったり、離れたり揺れながら（地球の公転軌道を横切りながら）、太陽の周りをまわっています。しかし、月は地球の周りをほぼ一定速度（赤い矢印）で回っていますので、地球の軌道の内側 （地球より太陽に近い位置）にいる時間と外側（地球より太陽から遠い位置）にいる時間は同じです。ということは、月が太陽の周りを回るときにはその速度が変化しているのでしょうか？そのとおりです。月が地球の外側にいるときにはその速度は速くなり、逆に地球の内側にいるときには遅くなるということです。この理由は、図で判るように（この図は、月の速度の方向が判りやすいように、月の軌道をあえてらせん状に書いています。）月が地球の外側にあるとき、月の進む方向が地球の進む方向と一致しているため地球の公転速度(青い矢印)に月の公転速度（外側の赤い矢印）が加わり速くなります。逆に、地球の内側にあるときには、月のすすも方向と地球の進む方向が逆になるため、地球の公転速度(青い矢印)から月の公転速度（内側の赤い矢印）を引いた速度になります。

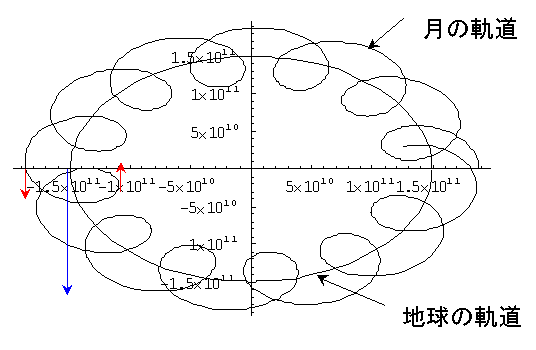
　これは月の公転軌道方向が地球の公転軌道方向と一致している場合にそうなります.逆に、地球の公転軌道方向と月の公転軌道方向が互いに逆向きのときには、下の図（こちらも、上と対比して分かりやすいようにらせんで書いています。）の様に月の軌道の軌跡は地球の軌道の外側のほうが短く、内側のほうが長くなります。

　さて、それでは、太陽の周りを回る月の速度と地球の速度はどのくらいなのでしょうか？本当ならば、重力から計算するのが正道ですが、ここでは、地球や月の軌道はあらかじめ決まっているものとして簡単な計算を行います。太陽の周りを回る地球の公転軌道半径はR=1.496x10¹¹m、公転周期はT=365.25日、地球の周りを回る月の公転軌道半径はｒ＝3.84ｘ10⁸m、公転周期はｔ＝27.327日です。従って、

　地球が太陽の周りを回る公転速度(青い矢印)は

　　　２πR/T=29800m/s

　月が地球の周りを回る公転速度（赤い矢印）は

　　　２πr/t=1022m/s

となりますから、この値を見ると、月が地球を回る速度より地球が太陽を回る速度のほうが圧倒的に、速いことがわかります。このことからも、 月が地球の進む方向と逆向きに進むこと、すなわち、らせん状に軌道を描くことはないことがわかります。そうです、実は今までの上の図は月の回る速度を100倍 にして描いていたのです。だから、月が地球の公転速度を超えて逆行し、らせんを描いたのです。（但し、物理学上は、月の速度が地球の公転速度を上回ると、月が地球の重力に打ち勝って飛び出してしまいます。）ですから、月が太陽の周りを回る公転速度は

　月が地球より外側にいるときは

２πR/T+２πr/t=30822m/s

　月が地球より内側にいるときは

２πR/T-２πr/t=28778m/s

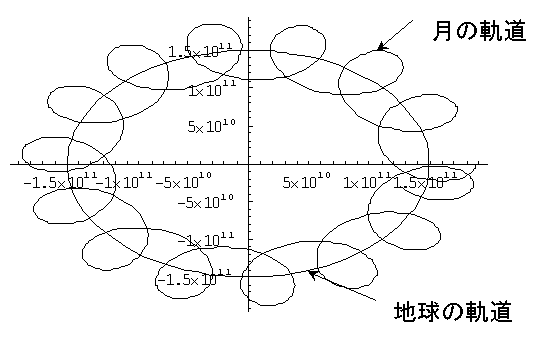
となり、実質的にはそんなに変わらないことになります。３％くらいの変動でしょう。地球と月の軌道をスケールをあわせて書くと以下の図のようになり、ほとんど変わらないことが判ります。ちなみに、上に書いたらせん状の図は判りやすさ優先のために書いたものです。

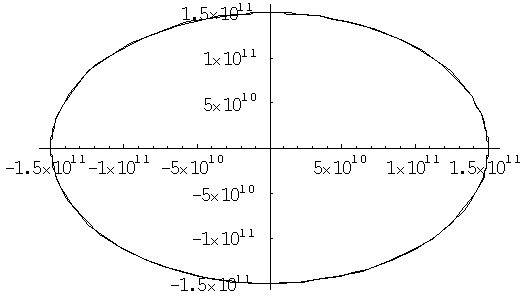
　さて、では、実際に月が地球の公転軌道の内側を走る距離と外側を走る距離はどのくらい違うでしょうか？ちょっと計算してみましょう。太陽、地球、そして月の位置関係を下の図のようだったとします。 ここでは、正確を記すためにらせん状ではなく、地球の軌道の周りを揺れているように書いています。

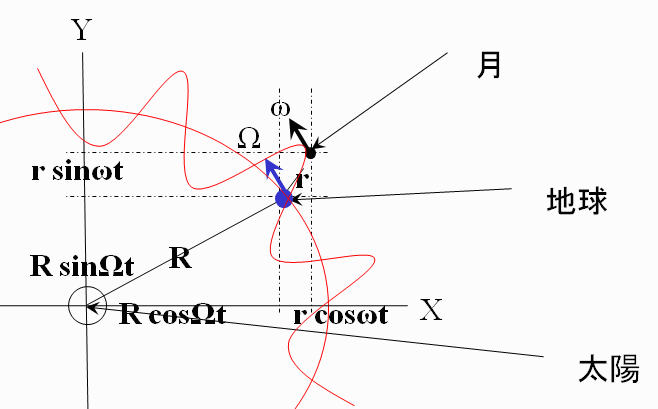
時刻０の時に太陽-地球-月が一直線に並び、X軸と一致していたとします。時刻ｔだけ経過して上の図のような位置関係になったときにの太陽と月の距離を求めます。

太陽と地球の距離（地球の公転軌道半径)はR=1.496x10¹¹m

地球が１日に太陽を回る角度（角速度)はΩ＝2π/365.25＝0.017344886976

そこで、X軸と地球のなす角度はΩｔになります。

地球と月の距離（月の公転軌道半径)はｒ＝3.84ｘ10⁸m、

月が１日に地球を回る角度(角速度)はω＝2π/27.327＝0.2299259087049

そこで、X軸と月のなす角度をωｔとなります。

この時、それぞれのX、Y軸方向の距離は

太陽と地球のX軸方向の距離はR cosΩt

地球と月のX軸方向の距離はr cosωt

太陽と地球のY軸方向の距離はR sinΩt

地球と月のY軸方向の距離はr sinωt

となるので、

X＝R cosΩt+r cosωt

Y＝R sinΩt+r sinωt

として月の軌道は

（X²+Y²)^1/2

となります。このがRより大きいときは月は地球の公転軌道の外側にいて、Rより小さいときは逆に内側にいることになります。そこで、上の式がRに等しいとして、その解を求めれば、月が地球の公転軌道を横切る時刻になります。そこで、

（X²+Y²)^1/2＝R

即ち、

（R cosΩt+r cosωt）²＋（R sinΩt+r sinωt）²＝R²

の解tを求めます。三角関数の解は無限にありますが、値の小さいほうから、月が地球の外側から内側に入るときの時刻t1＝7.390日、内側から外側に出る時刻t2＝22.147日、再び外側から内側に入る時刻t3＝36.927日の3つの解を得ます。そうすると、t2-t1＝14.756日が内側にいる時間、t3-t2＝14.781日が外側にいる時間になります。0.024日＝35分ほど違いますが、これは地球の公転軌道面を基準としたために内側の時間が短くなったのです。もし、公転軌道の接線を気準位すれば同じになるはずです。しかし、この35分の間に月は2.13x10⁶m移動しますが、この差は後の計算でも判る様に問題にはなりません。

　では、ここから本番です。さて、では,月が地l球の周りを一周する間に、地球の内側を走る距離と地球の外側を走る距離を求めてみましょう。一般的にある関数x=f(t),y=g(t)で表される曲線の長さLは以下の積分で求められます。

L=∫((df(t)/dt)²+(dg(t)/dt)²)^1/2 dt

従って、上のX、Yを当てはめ、積分を実行すると地球の内側を進む距離Linと外側を進む距離Loutはそれぞれ次のようになります。

Lin＝3.7156x10⁸m

Lout＝3.8879x10⁸m

内側を走る距離のほうが短いですね。しかもその距離の差Lout−Lin＝17.23x10⁶mは先ほどの35分間に動く距離よりも遥かに大きく、計算に問題を生じませんね。このように、月が太陽を回るときは地球の外側のほうが内側よりも長い距離走ることが判ります。ところで、前に述べた、地球と月が反対方向に公転している場合の走る距離を求めてみると、

Lin＝3.8592x10⁸m

Lout＝3.7684x10⁸m

となり、今度は内側のほうが長い距離を走ることになります。

いかがでしたか？