力の合成と分解について?
1999年11月17日に中学3年生の男の子からご質問を頂きました.。
質問があります是非教えてください。中学3年生です。私達の身の回りにある、力の合成や分解にかかわっている道具、器具、機械、おもちゃ、などがあったら教えてください。お願いします
こんにちは、ご質問ありがとうございます。 できれば、質問ページのフォームを利用していただければありがたいです。
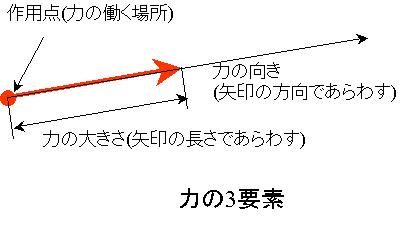
さて、中学3年生ですと力の合成分解を習うのですね。と言うことは、運動の法則についても習ってますね。力とはどういうものか?力の三要素である力の大きさ、力の向き、そして力が加わる作用点、また、力の単位とか弾性力なども習っていますね。 この力のように大きさと方向のあるものを下の図のように矢印で表しますが、この方向と大きさを持った矢印をベクトルと言います

では、本題の力の合成、分解にかかわる道具、器具、機械、おもちゃということですが....
まず、力の合成分解とはどういうことか考えてみましょう。同じ方向を向いていたら、2つ以上の力を、そのまま足したり引いたり(合成)、1つの力を同じ方向の2つ以上の力に分けたり(分解)できます。
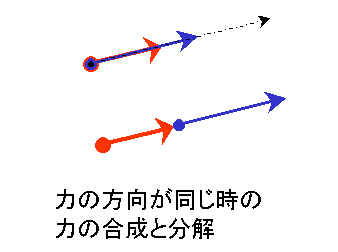
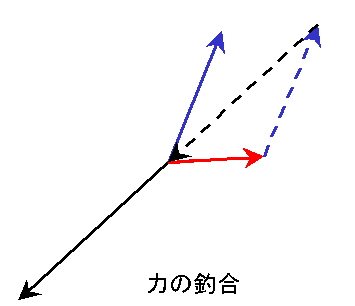
また、1つの力を違う方向の2つ以上の力に分ける(分解)こともできます。このとき、分解された力を順につなぎ合わせていくと、必ずもとの力と同じにならなければなりません(釣合)。逆に、2つ以上の違う方向の力を順につなげていって足すことができます。(合成) 力の合成や分解を考えるときは矢印をどんどんつなげていく、あるいは、矢印をどんどん引いていく、そういうことが重要です。
|
|
 |
このように、力の合成と分解は考え方だと言うことを理解してください。そういう意味では、力が働くものは、道具や器具、機械、おもちゃすべてどんなものでも力の合成と分解にかかわっています。
例えば、
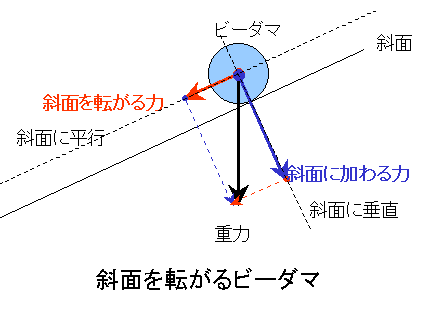
1.斜面を転がるビー玉 力の分解 学校の理科の時間に習った力の分解では、斜面を転がるビー玉について習ったでしょうか?斜面を転がるビー玉には重力が真下にっ働きますね。そして、その重力を斜面に平行な(斜面に沿った)方向と斜面に垂直な方向に分解することができますね。そして、斜面に平行な方向の力は斜面を転がる力に使われます。また、斜面に垂直な方向の力は斜面を滑らないようにする摩擦抵抗に使われます。ですから、斜面とか坂を使った道具、おもちゃすべて力の分解を考えると理解できますね。ミニ4駆に坂道があれば力の分解を利用できます。プラレールもそうでしょう
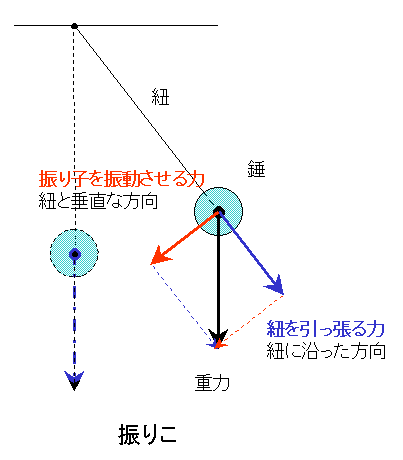
2.振り子 力の分解 今度は振り子を考えてみましょう。振り子も斜面を転がるビー玉と同じで、鉛直方向に重力が働きます。それを、ぶら下げた紐に沿った方向と、それに垂直な方向に分解します。すると、紐に沿った方向の力は紐との釣り合いを保っています。そうして、それに垂直な方向の力は振り子が振れるために使われます。さて、振り子が真下に来たときはどうでしょう?鉛直方向の力が紐のぶら下げる力とつりあって、振り子を振る力はなくなってしまいますね。ただ、慣性力(振り子の勢い)で、また振り子は振れていきますけど....このように振り子を利用するものも力の分解を考えに入れることができますね。昔あった振り子のついた柱時計なんかもそうですし、建物を壊すときに鉄球をぶつけますが、これも同じように考えることができますね。
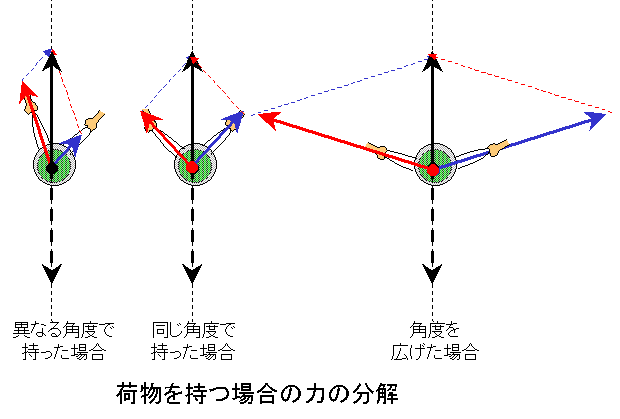
3.荷物 力の合成 さて、力の合成についてはどのように習いましたか?例えば、友達と2人でスイカを買いに行きました。スイカは重いですから、二人で持ちました。このとき、二人のスイカ持つ力を合成した力が真上に働き、スイカの重さとつりあうことがわかりますね。とこrで、下の真中の図のように二人が同じ角度でスイカを持ったときは、同じ力で済みます。ところが、左の図のように互いに異なる角度で持ったときには、荷物を持つ力は異なってきます。より垂直に近いほうが重くなりますね。逆に水平に近いほうが軽くなります。ですから、ちょっとずるをしようと思ったときには水平方向に少し引っ張るようにして持つとよいです。しかし、二人とも水平方向に引っ張ると今度は右の図のように引っ張る角度がどんどん開いて、二人とも重くなってしまいます。
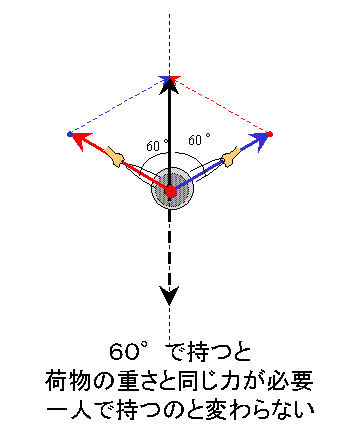
そして、二人の力が最も少なくて済むのは同じ方向に持ったときです。そうすると、たとえば4kgのスイカを二人で持つと、それぞれ2kgの力でもてます。ところが、下の図のように二人の持つ角度が垂直方向から60度になったらどうなるでしょう? 下の図でわかるように、合成するときの角度が全部60度で正三角形になります。すると、どの辺も同じ長さですから、二人とも4kgの力が必要になります。これなら一人でもったときと同じですね。
このように、物を持ったりぶら下げたりすることは力の合成にかかわります。和室に吊り下げてある蛍光灯は何本の鎖で吊り下げられていますか?この場合は荷物とはちょっと違いますが、やはり力を合成したり分解したりして考えることができます。
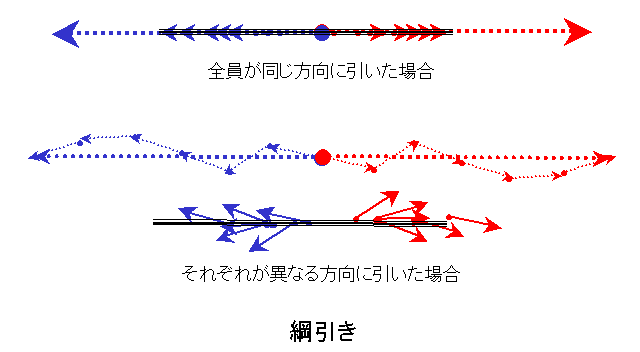
4.綱引き 力の合成 綱引きは判りやすいですね。何人もの人が力を合わせて(合成)綱を引きます。全員が同じ方向に引けば、下の図の上図のように全て足せばよいですね。それぞれが違う方向に引くと下の図の下図のように、その力の矢印を次々と足して最後に全体の力を合成することができます。ちなみに、足す順番にはよりません。全ての力の矢印を足せばよいのです。
5.パチンコ 力の合成 パチンコというおもちゃを知っていますよね。ピンと張ったゴムに玉を装着して飛ばす道具(おもちゃ)です。このパチンコのゴムはゴムに沿った方向に力が働きます。そして、その力が合成された方向に玉が飛び出しますね。
6.動滑車 力の分解 滑車は知っていますか?滑車は力の方向を変えます。動滑車は2つに力を分解します。この動滑車に張られたロープが同じ方向を向いていれば荷物を持つときと同じように半分の力で済みます(分解)。下の図のように真中の大きな丸い錘を二つの動滑車でぶら下げると、力が1/4になります。そうすると、右側の小さな錘の重さは大きな錘の重さの1/4で釣り合うことになります。もちろん滑車の重さは考えないのですよ。200kgあるお相撲さんを50kgの中学生で持ち上げることができてしまいます。滑車に掛かっているロープの角度が下の図では垂直方向ですから、単に重さを分けただけですが、そのロープに角度があると、その角度に見合った力に分解することができます。そういう意味では動滑車は力を分解して少ない力で物を持ち上げたりするのに使われます。最もいい例がクレーン車などではないでしょうか?

取りとめもなく書いてしまいましたが、力の働くものは、そのものに応じて分解したり合成したりすることは自由です。上手に力を分解したり、合成したりできれば何処にどのような力が働いているかとか、どのように動くかが良く判ります。機械設計や建築の現場などではその構造物の強度が重要になるので、力の合成や分解は何時も考えられています。身の回りの力が働いているものの合成とか分解を考えてみてはいかがでしょうか?
さて、ここからは実際に力を合成・分解したときに、その力がどのくらいの大きさか計算する方法を考えてみましょう。高校生になると判ると思います。ちょっと難しいので読み飛ばしてもかまいません。では、下の図を参考に考えて見ましょう。
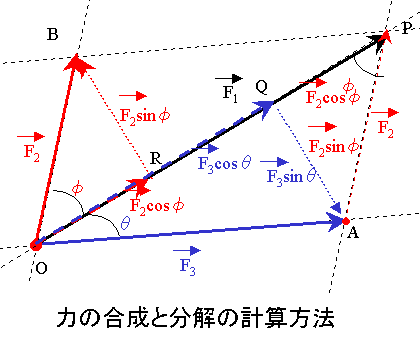
力の合成
まず、力の合成を考えてみます。赤い力の矢印(ベクトル) F2 と青い力の矢印(ベクトル) F3を合成しましょう。ベクトルの式で書くと下のようになります。
→ → →
F2+F3=F1
まず、補助線を引きます。青いF3(OA)の矢印の先端に赤いF2(OB)と平行に補助線(AP)を、また、逆に青いF3と平行に赤いF2の矢印の先端に補助線(BP)を引きます。そうすると、平行四辺形(OAPB)ができます。この平行四辺形の対角線(OP)の方向が合成された力F1の方向になり、このOPの長さがF1の大きさになります。ですから、このF1の長さを計算すればよいのです。ところで、このOPの長さというのは、F2+のOP方向の成分とF3のOP方向の成分の和ですから、
∠AOP=θ
∠BOP=φ
とすれば、
F1=F2cosφ+F3cosθ1 (1)
となります。また、OPに垂直な方向の力はつりあっていますので、
F2sinφ=F3cinθ1 (2)
であることが判ります。
力の分解
さて、今度は逆に、F1
を任意φとθの方向に分解しましょう。さっきの力の合成の場合とまったく逆の形で、(1)式と(2)式からF2とF3を求めれば良いのです。答えだけを書くと、
F2=F1tanφtanθ/(tanφ+tanθ) /sinφ
F3=F1tanφtanθ/(tanφ+tanθ) /sinθ
となります。